Thomasguo666的小屋

设

$S_i=\sum_{j=1}^ia_i$

我们可以先列一个简单的dp方程:

$f(i)=\min_{j=1}^{i-1} \{A(S_i-S_j)^2+B(S_i-S_j)+C\}$

先去掉$min$符号，然后整理：

$2AS_iS_j-AS_i^2-BS_i-C+f(i)=f(j)+AS_j^2-BS_j$

我们把所有与$i$有关的全部项移到左边，其余移到右边。并且以$j$为主元，把$j$和$S_j$等看作变量，其余看作常数。然后我们确保$2AS_i$为正数。（为了方便，我们把$A$，$B$，$C$均乘以$-1$，然后求$f(i)$的最小值）

我们让一条斜率为$2AS_i$的直线依次经过这$i-1$个点，然后找到使它在$y$轴上的截距最小的点即可。

注意到当直线$P_{j-1}P_j$的斜率大于$P_jP_{j+1}$时，$P_j$一定不是我们要找的点，所以我们可以用单调队列来维护所有的决策点，每次插入一个新决策点时，先检查它与队首构成的直线的斜率，以及队首的两个点构成的直线的斜率，如果不对就把队首扔掉，并继续。（详见代码）

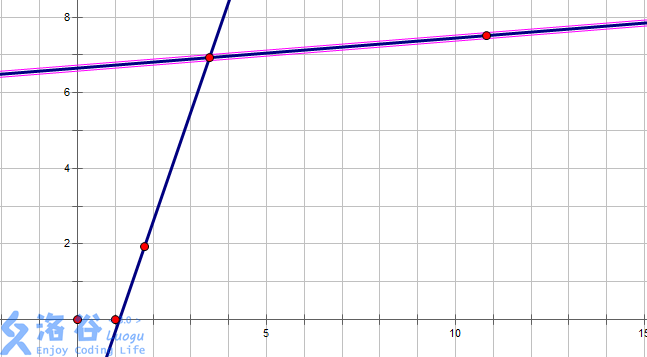
这个不对

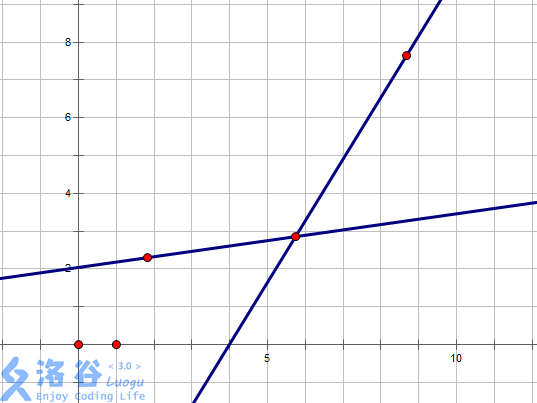
这个对

并且，如果$P_{j-1}Pj$的斜率大于$2AS_i$，说明$P_{j-1}$优于$P_j$。如果$P_jP_{j+1}$的斜率小于$2AS_i$，说明$P_{j+1}$优于$P_j$。因此，如果有三个点$P_{j-1}$,$P_j$,$P_{j+1}$，满足$K_{P_{j-1}P_j}<2AS_i\leq K_{P_jP{j+1}}$，那么$P_j$就是最优决策点。在本题中，由于$2AS_i$单调递增，所以若$P_jP_{j+1}$的斜率小于$2AS_i$，就可以把$P_j$扔掉，这样队尾永远是当前最优的决策点。但是，在某些问题中，斜率并不是单调递增的，这时不能把队尾扔掉，而是每次要使用二分查找的技巧，找到第一条斜率不小于$2AS_i$的直线。

然后就看代码吧：

#include <bits/stdc++.h>
#define debug printf("Running %s on line %d...\n",__FUNCTION__,__LINE__)
#define in inline
#define re register
#define sqr(i) (ll((i))*(i))
#define F(i) (A*sqr(s[(i)])-B*s[(i)]+f[(i)])
using namespace std;
typedef long long ll;
typedef double db;
in int read()
{
    int ans=0,f=1;char c=getchar();
    for (;!isdigit(c);c=getchar()) if (c=='-') f=-1;
    for (;isdigit(c);c=getchar()) ans=(ans<<3)+(ans<<1)+(c^48);
    return ans*f;
}
int a[1000005],s[1000005];
int q[1000005],l,r;
ll f[1000005];
ll A,B,C;
// f(i)=f(j)+A(s[i]-s[j])^2+B(s[i]-s[j])+C
//     =f(j)+A*s[i]^2-2As[i]s[j]+As[j]^2+Bs[i]-Bs[j]+C
// 2As[i]s[j]-As[i]^2-Bs[i]-C+f(i)=f(j)+As[j]^2-Bs[j]
int main()
{
    int n=read();
    A=-read(),B=-read(),C=-read();
    for (int i=1;i<=n;i++) a[i]=read(),s[i]=s[i-1]+a[i];
    l=r=1;
    for (int i=1;i<=n;i++)
    {
        while (r>l && (F(q[l+1])-F(q[l]))<2*A*s[i]*(s[q[l+1]]-s[q[l]])) l++;
        f[i]=f[q[l]]+A*sqr(s[i]-s[q[l]])+B*(s[i]-s[q[l]])+C;
        while (r>l && (F(q[r])-F(q[r-1]))*(s[i]-s[q[r]])>(F(i)-F(q[r]))*(s[q[r]]-s[q[r-1]])) r--;
        q[++r]=i;
    }
    cout<<-f[n]<<endl;
    return 0;
}