神仙数学题

事实上，我们可以对每头牛向谷仓做切线。记第$i$头牛向谷仓做切线的两个切点在这头牛这侧所加的弧为$l_i$

那么如果第$i$头牛和第$j$头牛可以互相看到，则$l_i$和$l_j$有交点。

于是接下来我们要解决两个问题：即如何表示和计算这$n$个弧，以及如何求出这$n$个弧中有多少对弧相交。

注意到圆心在$(0,0)$处，所以我们可以用一个弧的两个端点与原点的连线与$x$轴正半轴的夹角表示这个弧。

下规定小的角度为左端点，大的角度为右端点。

我们可以先求出牛与原点的连线与$x$轴正半轴的夹角$\angle AOB$，然后再计算两个端点与原点的连线与牛与原点的连线的夹角$\angle AOC$。

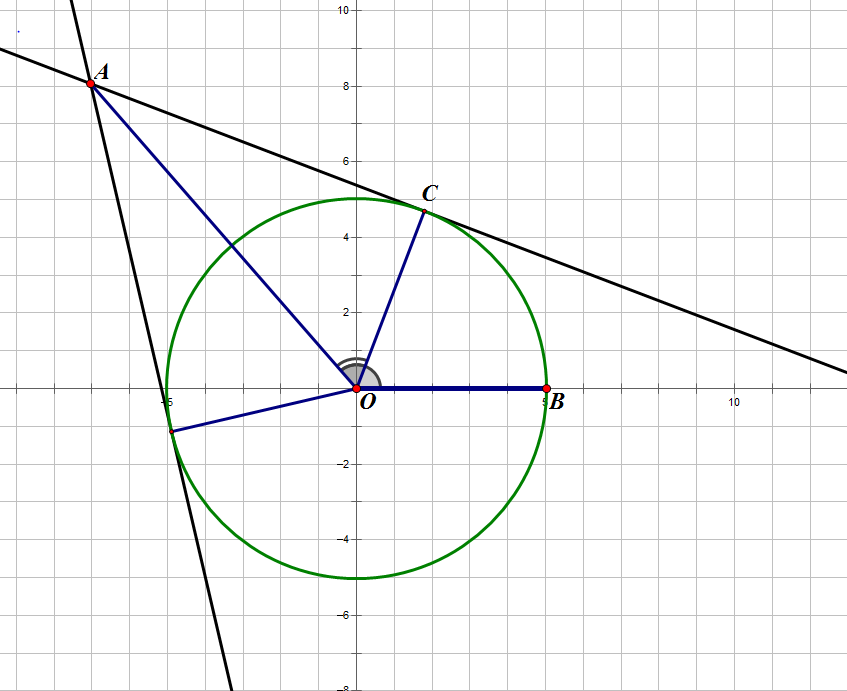
这样左右端点就分别为$\angle AOB \pm \angle AOC$

db r,pi=acos(-1);
struct point
{
    db x,y;
} a[100005];
struct seg
{
    db l,r;
    bool operator < (const seg &rhs) const
    {
        return l<rhs.l;
    }
} s[200005];
point o={0,0};
db dis(point a,point b)
{
    return sqrt(pow(a.x-b.x,2)+pow(a.y-b.y,2));
}
db angle(point a)
{
    return atan2(a.y,a.x);
}
seg get(point a)
{
    db l=dis(a,o);
    db ang=angle(a); 
    db ang2=acos(r/l);
    if (ang-ang2<0) ang+=2*pi;
    return (seg){ang-ang2,ang+ang2};
}

接下来就是要求有多少对弧相交。

第一步，破环为链（显然的）。

也就是对每个弧，把它的两个端点都加上$2\pi$当作一个新的弧。

第二步，把每个弧按照左端点排个序。

第三部：维护一个堆，其中堆顶元素的右端点最小。对于一段弧$l_i$

• 把堆里所有右端点比$l_i$的右端点小的弧全部弹出（因为这些弧不会再与以后的任意一个弧相交）
• 剩下的都与$l_i$相交。把答案加上堆的大小。
• 如果$i\leq n$即这个弧是原有的弧，那么就把这个弧加入堆中。

struct cmp
{
    bool operator () (seg a,seg b)
    {
        return a.r>b.r;
    }
};
int main()
{
	n=read(),r=read();
	long long ans=0;
	for (int i=1;i<=n;i++) a[i].x=read(),a[i].y=read();
	for (int i=1;i<=n;i++) s[i]=get(a[i]);
	for (int i=1;i<=n;i++) s[i+n]=(seg){s[i].l+2*pi,s[i].r+2*pi};
	sort(s+1,s+2*n+1);
	priority_queue<seg,vector<seg>,cmp> q;
	for (int i=1;i<=2*n;i++)
	{
	    while (q.size() && q.top().r<=s[i].l) q.pop();
	    ans+=q.size();
	    if (i<=n) q.push(s[i]);
    }
    cout<<ans<<endl;
    return 0;
}