浅谈珂学数据结构——珂朵莉树
珂朵莉树
珂朵莉树是一种基于平衡树的暴力数据结构。一般用std::set来实现。
什么时候用珂朵莉树:
- 当有区间赋值操作时
- 当有区间幂次和等线段树树状数组显然不能胜任的操作时
定义
珂朵莉树是把连续的一段值相同的区间当作一个节点对待。下面是一个节点的定义
typedef long long ll;
struct node
{
int l,r;//节点的左、右端点
mutable ll v;//如果不加mutable修饰符,那么v变量初始化后就不能修改了。
node (int l,int r=-1,ll v=0):l(l),r(r),v(v) {}//构造函数
bool operator <(const node &rhs) const
{
return l<rhs.l;
}
};
set<node> s;
基本操作
初始化
for (int i=1;i<=n;i++) s.insert(node(i,i,a[i]));
重要:区间分裂
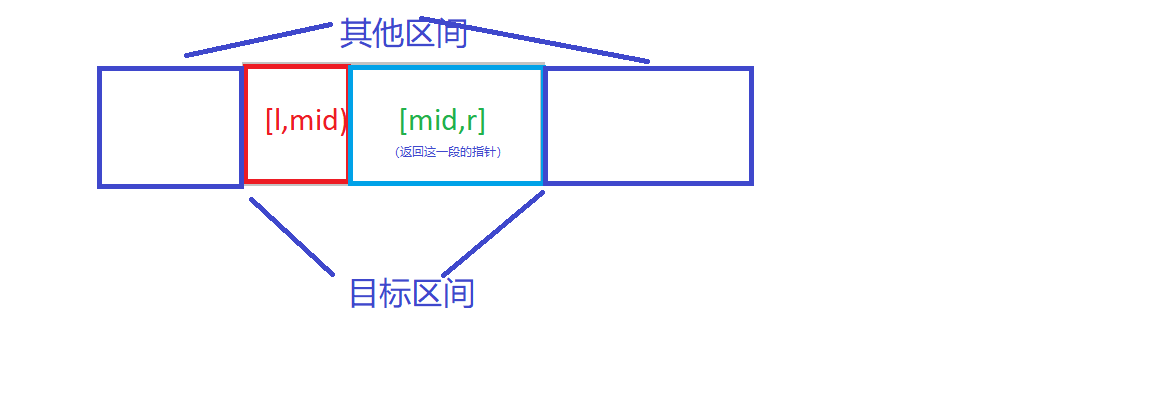
就是把包含mid的区间[l,r]分裂成[l,mid-1]和[mid,r],并返回[mid,r]的指针。
具体来讲,是先把区间[l,r]删去,再分别把区间[l,mid),和[mid,r]加入。
typedef set<node>::iterator IT;
IT split(int mid)
{
IT it=s.lower_bound(node(mid));//寻找第一个左端点大于等于k的区间。
if (it!=s.end()&&it->l==mid) return it; //如果找到的这个区间的左端点就是mid那么就返回这个区间的指针。
--it;//否则mid一定在上一个区间里
int l=it->l,r=it->r;
ll v=it->v;
s.erase(it);//删掉区间[l,r]
s.insert(node(l,mid-1,v));//插入区间[l,mid-1]
return s.insert(node(mid,r,v)).first; //s.insert()返回的其实是一个pair,其中的first是变量的指针。
}
核心:区间赋值
就是把区间[l,r]的值全都改为v。
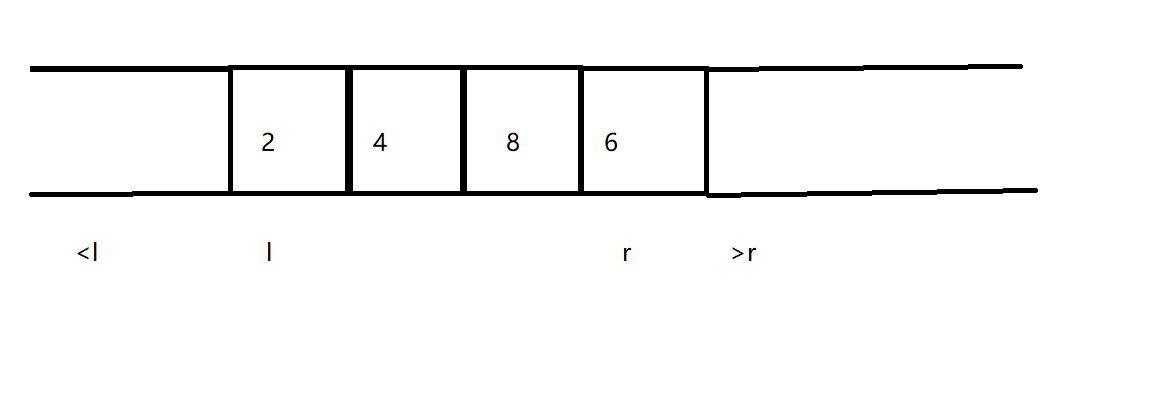
区间赋为5后
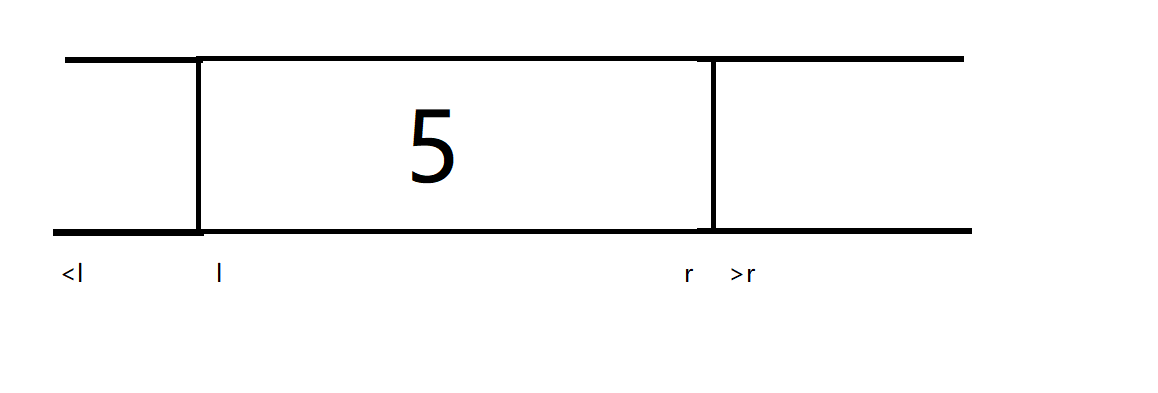
void assign(int _l,int _r,ll v)
{
IT r=split(_r+1),l=split(_l); //重点!一定要按照这个次序,否则可能会导致指针失效而RE,下同
s.erase(l,r); //删除区间[l,r+1),是一个方便但比较少见的操作
s.insert(node(_l,_r,v));
}
这个操作直接使set的大小接近n/k。具体证明见这里。但是如果不保证数据随机,那这玩意八成要GG。
其他的操作就可以用暴力了,这里讲几个常见的。
区间加
直接加就行了,十分暴力
void add(int _l,int _r,ll v)
{
IT r=split(_r+1),l=split(_l);
for (;l!=r;l++) l->v+=v;
}
区间k小值
把区间里每段拿出来排个序就行了。
ll kth(int _l,int _r,int k)
{
IT r=split(_r+1),l=split(_l); //把区间里
vector<pair<ll,int> > v;
v.clear();
for (;l!=r;l++) v.push_back(pair<ll,int>(l->v,l->r-l->l+1));// 每段拿出来
sort(v.begin(),v.end());// 排个序
for (vector<pair<ll,int> >::iterator it=v.begin();it!=v.end();it++)
{
k-=it->second;
if (k<=0) return it->first; //就行了
}
}
区间幂次和
直接快速幂就行了。
ll sum(int _l,int _r,int x,int y)
{
IT r=split(_r+1),l=split(_l);
ll ans=0;
for (;l!=r;l++)
{
ans=((ans+(ll)(l->r-l->l+1)*qpow(l->v,(ll)x,(ll)y))%y+y)%y;
}
return ans;
}
从以上几个操作我们可以看出,珂朵莉树不仅有代码量小,易调试的优点,并且还可以解决许多线段树树状数组等数据结构无法(或难以)胜任的问题。
例题:
CF896C 模板题
代码:
#include <bits/stdc++.h>
#define IT set<node>::iterator
using namespace std;
typedef long long ll;
int p=1000000007;
ll qpow(ll a,ll k,ll p)
{
a%=p;
ll ans=1;
while (k)
{
if (k&1) ans=ans*a%p;
a=a*a%p;
k>>=1;
}
return ans;
}
struct node
{
int l,r;
mutable ll v;
node (int l,int r=-1,ll v=0):l(l),r(r),v(v) {}
bool operator <(const node &rhs) const
{
return l<rhs.l;
}
};
set<node> s;
IT split(int k)
{
IT it=s.lower_bound(node(k));
if (it!=s.end()&&it->l==k) return it;
--it;
int l=it->l,r=it->r;
ll v=it->v;
s.erase(it);
s.insert(node(l,k-1,v));
return s.insert(node(k,r,v)).first;
}
void add(int _l,int _r,ll v)
{
IT r=split(_r+1),l=split(_l);
for (;l!=r;l++) l->v+=v;
}
void assign(int _l,int _r,ll v)
{
IT r=split(_r+1),l=split(_l);
s.erase(l,r);
s.insert(node(_l,_r,v));
}
ll kth(int _l,int _r,int k)
{
IT r=split(_r+1),l=split(_l);
vector<pair<ll,int> > v;
v.clear();
for (;l!=r;l++) v.push_back(pair<ll,int>(l->v,l->r-l->l+1));
sort(v.begin(),v.end());
for (vector<pair<ll,int> >::iterator it=v.begin();it!=v.end();it++)
{
k-=it->second;
if (k<=0) return it->first;
}
}
ll sum(int _l,int _r,int x,int y)
{
IT r=split(_r+1),l=split(_l);
ll ans=0;
for (;l!=r;l++)
{
ans=((ans+(ll)(l->r-l->l+1)*qpow(l->v,(ll)x,(ll)y))%y+y)%y;
}
return ans;
}
int n,m;
ll seed,vmax;
ll a[100005];
ll rnd()
{
ll ans=seed;
seed=(seed*7+13)%p;
return ans;
}
int main()
{
cin>>n>>m>>seed>>vmax;
for (int i=1;i<=n;i++) a[i]=(rnd()%vmax)+1,s.insert(node(i,i,a[i]));
s.insert(node(n+1,n+1,0));
for (int i=1;i<=m;i++)
{
int op=int(rnd()%4)+1,l=int(rnd()%n)+1,r=int(rnd()%n)+1,x,y;
if (l>r) swap(l,r);
if (op==3) x=int(rnd()%(r-l+1))+1;
else x=int(rnd()%vmax)+1;
if (op==4) y=int(rnd()%vmax)+1;
if (op==1) add(l,r,ll(x));
else if (op==2) assign(l,r,ll(x));
else if (op==3) cout<<kth(l,r,x)<<endl;
else cout<<sum(l,r,x,y)<<endl;
}
return 0;
}
软件包管理器 树链剖分,吸口氧能过
代码:
//luogu-judger-enable-O2
#include <bits/stdc++.h>
using namespace std;
inline int read()
{
char c=getchar();int ans=0;
for (;!isdigit(c);c=getchar());
for (;isdigit(c);c=getchar()) ans=(ans<<3)+(ans<<1)+c-48;
return ans;
}
int dep[100005],top[100005],l[100005],sz[100005],fa[100005],son[100005],b[100005],a[100005];
vector<int> G[100005];
void dfs1(int u)
{
sz[u]=1;
for (register int i=0;i<G[u].size();i++)
{
int v=G[u][i];
if (v==fa[u]) continue;
dep[v]=dep[u]+1,fa[v]=u;
dfs1(v),sz[u]+=sz[v];
if (sz[v]>sz[son[u]]) son[u]=v;
}
}
int tot=0;
void dfs2(int u,int h)
{
l[u]=++tot,a[tot]=b[u],top[u]=h;
if (!son[u]) return ;
dfs2(son[u],h);
for (register int i=0;i<G[u].size();i++)
{
int v=G[u][i];
if (v==fa[u] || v==son[u]) continue;
dfs2(v,v);
}
}
struct node
{
int l,r;
mutable int v;
node (int l,int r=-1,int v=0):l(l),r(r),v(v) {}
bool operator < (const node &rhs) const
{
return l<rhs.l;
}
};
set<node> s;
typedef set<node>::iterator IT;
inline IT split(int k)
{
IT it=s.lower_bound(node(k));
if (it!=s.end() && it->l==k) return it;
--it;
int l=it->l,r=it->r,v=it->v;
s.erase(it);
s.insert(node(l,k-1,v));
return s.insert(node(k,r,v)).first;
}
inline int assign(int l,int r,int v)
{
IT rp=split(r+1),lp=split(l);
int before=0,after=(r-l+1)*v;
for (register IT it=lp;it!=rp;it++) before+=(it->r-it->l+1)*(it->v);
s.erase(lp,rp);
s.insert(node(l,r,v));
return abs(after-before); //assign的同时要计算改变了多少个安装包的状态。
}
inline int install(int u,int v)
{
int ans=0;
while (top[u]!=top[v])
{
if (dep[top[u]]<dep[top[v]]) swap(u,v);
ans+=assign(l[top[u]],l[u],1);
u=fa[top[u]];
}
if (dep[u]>dep[v]) swap(u,v);
ans+=assign(l[u],l[v],1);
return ans;
}
inline int uninstall(int u)
{
return assign(l[u],l[u]+sz[u]-1,0);
}
inline void addedge(int u,int v)
{
G[u].push_back(v),G[v].push_back(u);
}
int main()
{
int n,m;
n=read();
s.insert(node(1,n+1,0));
for (register int i=2;i<=n;i++) addedge(i,read()+1);//所有软件包编号加一,方便计算。
m=read();
dfs1(1);
dfs2(1,1);
for (register int i=1;i<=m;i++)
{
char opt[20];
scanf("%s",opt);
int x=read();
if (opt[0]=='i') printf("%d\n",install(x+1,1));
else printf("%d\n",uninstall(x+1));
}
return 0;
}
染色 同样是树链剖分,然而比较困难的地方在于信息的整合,看注释:
代码:
#include <bits/stdc++.h>
using namespace std;
int read()
{
char c=getchar();int ans=0,f=1;
for (;!isdigit(c);c=getchar()) if (c=='-') f=-1;
for (;isdigit(c);c=getchar()) ans=(ans<<3)+(ans<<1)+c-48;
return ans*f;
}
struct data
{
int lc,rc,len;
data (int lc=0,int rc=0,int len=0):lc(lc),rc(rc),len(len) {};
data operator + (const data &rhs) const //整合信息
{
data ans;
if (!len) return rhs;
if (!(rhs.len)) return data(lc,rc,len); //如果有一段长度为0,就返回另一段
if (rc==rhs.lc) ans.len=len+rhs.len-1; //如果两段的端点是一种颜色,那么段数减一
else ans.len=len+rhs.len; //否则段数不变
ans.lc=lc,ans.rc=rhs.rc;
return ans;
}
};
struct node
{
int l,r;
mutable int v;
node (int l,int r=-1,int v=0):l(l),r(r),v(v) {}
bool operator < (const node &rhs) const
{
return l<rhs.l;
}
};
set<node> s;
typedef set<node>::iterator IT;
IT split(int k)
{
IT it=s.lower_bound(node(k));
if (it!=s.end() && it->l==k) return it;
--it;
int l=it->l,r=it->r,v=it->v;
s.erase(it);
s.insert(node(l,k-1,v));
return s.insert(node(k,r,v)).first;
}
void assign(int l,int r,int v)
{
IT rp=split(r+1),lp=split(l);
s.erase(lp,rp);
s.insert(node(l,r,v));
}
data query(int l,int r)
{
IT rp=split(r+1),lp=split(l);
data ans;
for (IT it=lp;it!=rp;it++)
{
ans=ans+data(it->v,it->v,1);
}
return ans;
}
int l[100005],fa[100005],son[100005],dep[100005],sz[100005],top[100005],a[100005],b[100005];
vector<int> G[100005];
void dfs1(int u)
{
sz[u]=1;
for (int i=0;i<G[u].size();i++)
{
int v=G[u][i];
if (sz[v]) continue;
dep[v]=dep[u]+1,fa[v]=u;
dfs1(v),sz[u]+=sz[v];
if (sz[v]>sz[son[u]]) son[u]=v;
}
}
int tot=0;
void dfs2(int u,int h)
{
l[u]=++tot,a[tot]=b[u],top[u]=h;
if (!son[u]) return;
dfs2(son[u],h);
for (int i=0;i<G[u].size();i++)
{
int v=G[u][i];
if (v!=fa[u]&&v!=son[u]) dfs2(v,v);
}
}
void upd(int u,int v,int k)
{
while(top[u]!=top[v])
{
if (dep[top[u]]<dep[top[v]]) swap(u,v);
assign(l[top[u]],l[u],k);
u=fa[top[u]];
}
if (dep[u]>dep[v]) swap(u,v);
assign(l[u],l[v],k);
}
int qnum(int u,int v)
{
data a,b; //a负责存储u这边的信息,b负责存储v这边的信息,讨厌的地方在于不能swap
while (top[u]!=top[v])
{
if (dep[top[u]]<dep[top[v]]) b=query(l[top[v]],l[v])+b,v=fa[top[v]];
else a=query(l[top[u]],l[u])+a,u=fa[top[u]];
}
if (dep[u]>dep[v]) a=query(l[v],l[u])+a;
else b=query(l[u],l[v])+b;
swap(a.lc,a.rc);
return (a+b).len;
}
void addedge(int u,int v)
{
G[u].push_back(v),G[v].push_back(u);
}
int main()
{
int n=read(),m=read();
for (int i=1;i<=n;i++) b[i]=read();
for (int i=1;i<n;i++) addedge(read(),read());
dfs1(1);
dfs2(1,1);
for (int i=1;i<=n;i++) s.insert(node(i,i,a[i]));
for (int i=1;i<=m;i++)
{
char opt;
int x,y,z;
opt=getchar(),x=read(),y=read();
if (opt=='C')
{
z=read();
upd(x,y,z);
}
else printf("%d\n",qnum(x,y));
}
return 0;
}
完结撒花!!!★,°:.☆( ̄▽ ̄)/$:.°★ 。
(P.S. 按照yfz的说法,有一种复杂度正确的ODT,然而我不会……)
(再P.S. 如果窝学会了这个东西会找时间写的)