Thomasguo666的小屋

前置芝士：堆优化Dijkstra/优先队列bfs（其实本质上相同）

简介

A*算法是一种常见的搜索算法，可以用于在搜索中更快找到并判定最优解。

概念

最短路问题，大家应该都会解吧。堆优化dij其实就是优先队列bfs。

但是，优先队列bfs的策略有一个缺点：当前代价最小的状态，接下来可能有很大的代价。这就导致了最优解可能反而出现的比较晚。

于是我们很自然地想到一个对策：定义一个估价函数$f(x)$，表示状态$x$到最终状态的代价的估计值，而每次从堆中取出并扩展的是**“当前代价+估值”最小**的状态。并且，每个状态第一次出队，就是初始状态到它的最优解。

而这个估价函数$f(x)$有一个很重要的性质：假设$g(x)$为状态$x$到最终状态的实际值，则：

$f(x)\leq g(x)$

为什么呢？我们举个例子看看：（$w$是边权）

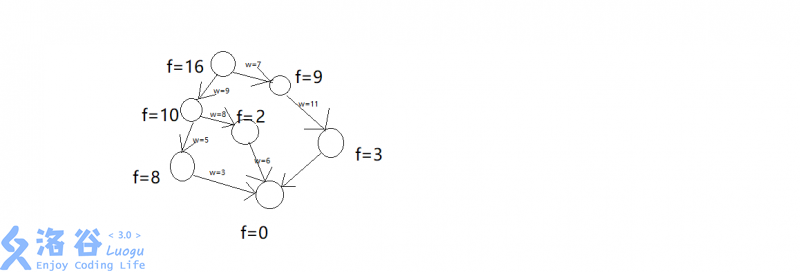
显然，最短路应该是走最左边这条，代价为$9+5+3=17$，但是由于这条边上的估值都被过大的估计导致结果算错（算出来是$9+8+6=23$）

而如果保证$f(x)\leq g(x)$，则即使某非最优解搜索路径上的状态$s$，由于估值不够准确，先被扩展了，但是：

• 由于$s$并非最优，故随着当前代价不断累加，总有一时刻s的当前代价大于从初始状态到目标状态的最小代价。
• 在最优解搜索路径上的状态$t$，由于$f(t)\leq g(t)$，故$t$的当前代价加上$f(t)$小于等于从初始状态到目标状态的最小代价。

综上所述，$t$将会被取出并扩展，并得到最优解。（在本文中请区分“扩展”与“被扩展”）

而且我们可以想到，f(x)越接近g(x)，就能越快找到最优解。

这种带估值函数的优先队列bfs，就是A*。

接下来我们通过几个例子，讲一讲A*估值函数的设计。

估值函数

先看一道例题：

集合位置

题意：求$1$号点到$n$号点的次短路长度。

我们已经说过，每个状态第一次出队，就是初始状态到它的最小代价。事实上，每个状态第$k$次出队，就是初始状态到它的第$k$小代价。(由数学归纳法)

并且每个状态的第$k$小代价，必是由某一个出队$k-1$次的状态扩展得到的。

证明：

由于每个状态第$k$次出队，就是初始状态到它的第$k$小代价$(k\in N^+)$，故对于一个已出队$k$次的状态$i$，由于另一个最小的被出队$k$次并能扩展到$i$的状态$j$扩展到$i$的当前代价，必然比任意一出队$k+1$次的状态$l$扩展到$i$的当前代价低（该代价必然比出队$k$次的$l$扩展到$i$的当前代价大），又比任意一出队$k-1$次的状态扩展到$i$的代价要大，故当前代价就是初始状态到$i$的第$k+1$小代价，是由出队$k$次的$j$扩展得到的。

综上所述，就是初始状态到每个状态的第$k$小代价，是由一个出队$k-1$次的状态扩展得到的。

故控制每个节点出队不超过$2$次，$n$号节点第$2$次出队时的代价就是次短路。

一个注意点：每个节点最多扩展一次，入队一次，出队两次。

那么现在我们需要设计一个估值函数。

然后发现，直接令$f(x)$为$x$到$n$的最短路即可。

#include <bits/stdc++.h>
using namespace std;
typedef double db;
db x[205],y[205],f[205];
int vis[205];
struct dat
{
    int u;
    db w;
    bool operator < (const dat &rhs) const {
        return w>rhs.w;
    }
};
struct ndat //注意：不仅要存储每个节点的当前代价+f(x)，还要存储该搜索路径上的每个节点的访问情况。每个节点最多访问一次！
{
    int u;
    db w;
    int vis[205];
    ndat (int u,db w):u(u),w(w) {
        memset(vis,0,sizeof(vis));
    }
    bool operator < (const ndat &rhs) const {
        return w>rhs.w;
    }
};
inline double a(int i,int j)
{
    return sqrt(pow(x[i]-x[j],2)+pow(y[i]-y[j],2));
}
vector<int> G[205];
void addedge(int i,int j)
{
    G[i].push_back(j);
    G[j].push_back(i);
}
int main()
{
    int n,m,tot=0;
    db ans=-1;
    cin>>n>>m;
    for (int i=1;i<=n;i++) cin>>x[i]>>y[i];
    for (int i=1;i<=m;i++)
    {
        int u,v;
        cin>>u>>v;
        addedge(u,v);
    }
    memset(f,127,sizeof(f));
    f[n]=0;
    priority_queue<dat> Q;
    priority_queue<ndat> q;
    Q.push((dat){n,0});
    while (!Q.empty()) //先预处理处每个节点的f(x)
    {
        dat p=Q.top();Q.pop();
        int u=p.u;
        if (vis[u]) continue;
        vis[u]=1;
        for (int i=0;i<G[u].size();i++)
        {
            int v=G[u][i];
            if (f[u]+a(u,v)<f[v])
            {
                Q.push((dat){v,f[u]+a(u,v)});
                f[v]=f[u]+a(u,v);
            }
        }
    }
    q.push((ndat){1,f[1]});
    while (!q.empty())
    {
        ndat p=q.top();q.pop();
        int u=p.u;
        db w=p.w-f[u];
        if (u==n) ++tot;
        if (tot==2)
        {
            ans=w;
            break;
        }
        for (int i=0;i<G[u].size();i++)
        {
            int v=G[u][i];
            if (p.vis[v]) continue; //如果当前搜索路径上访问过该点，则不必再次访问
            ndat nv=p;
            nv.u=v;
            nv.w=w+a(u,v)+f[v];
            nv.vis[v]=1;
            q.push(nv);
        }
    }
    (ans<0)?printf("%d\n",-1):printf("%.2f",ans);
    return 0;
}

利用这个思路，我们还可以解决$k$短路问题

对于题目中的“总能量”条件，其实和总数量（即$k$）是一样的。转化一下即可。

(顺便说一句，这题不知道怎么回事恶意卡A*，非要用左偏树可并堆来做。在我看来这是一种无聊而可恶的行径，没有什么教育意义。前面的都是屁话，最重要的是，不让我们多A一道题)

这道题并不需要控制每个状态访问的次数。

// luogu-judger-enable-o2
#include <bits/stdc++.h>
using namespace std;
typedef double db;
db dis[5005],f[5005];
int t[5005],vis[5005];
struct dat
{
    int u;
    db w;
    bool operator < (const dat &rhs) const {
        return w>rhs.w;
    }
};
vector<dat> G[5005],g[5005];
void addedge(int i,int j,db w)
{
    G[i].push_back((dat){j,w});
    g[j].push_back((dat){i,w});
}
int main()
{
    int n,m,ans=0;
    db e;
    cin>>n>>m>>e;
    if (e>1000000)
    {
        cout<<"2002000"<<endl;
        return 0;
    }
    for (int i=1;i<=m;i++)
    {
        int u,v;
        db w;
        cin>>u>>v>>w;
        addedge(u,v,w);
    }
    memset(f,127,sizeof(f));
    f[n]=0;
    priority_queue<dat> q,Q;
    Q.push((dat){n,0});
    while (!Q.empty())
    {
        dat p=Q.top();Q.pop();
        int u=p.u;
        if (vis[u]) continue;
        vis[u]=1;
        for (int i=0;i<g[u].size();i++)
        {
            dat v=g[u][i];
            if (f[u]+v.w<f[v.u])
            {
                Q.push((dat){v.u,f[u]+v.w});
                f[v.u]=f[u]+v.w;
            }
        }
    }
    q.push((dat){1,f[1]});
    while (!q.empty())
    {
        dat p=q.top();q.pop();
        int u=p.u;
        db w=p.w-f[u];
        if (u==n)
        {
            e-=w;
            if (e>=1e-6) ans++;
            else break;
            continue;
        }
        for (int i=0;i<G[u].size();i++)
        {
            dat v=G[u][i];
            q.push((dat){v.u,w+v.w+f[v.u]});
        }
    }
    cout<<ans<<endl;
    return 0;
}

A*的另一个应用就是8数码问题

我们发现，无论是多么好的策略，从一个状态到目标状态的代价，都不会低于该状态中每个数不为$0$的数$x$到目标状态中的$x$的曼哈顿距离之和。故我们可以把估价函数设为这个和。即：

$f(state)=\sum_{i=1}^8(|state.col_i-end.col_i|+|state.row_i-end.row_i|)$

并且，不同于$k$短路问题，每个状态最多扩展一次。即一个状态第二次被取出，就可以直接把它扔掉了。（这其实是正常A*的套路。）

如何判定一个状态是否扩展过呢？这里直接使用$std::map$进行判定。不过，有一种叫康托展开的方法可以把1~9的全排列映射成1~362880的正整数（0~8当然也行），请自行翻题解百度。

代码：

#include <bits/stdc++.h>
#define in inline
using namespace std；
// lyd /-\|<|O|
const int end=123804765；
map<int，int> vis；
int d[4]={-3，-1，1，3}；//四个方向
int pow10[]={
    1，10，100，1000，10000，100000，1000000，10000000，100000000
}；
in int get(int x，int p) //获取x的右数第p为
{
    return int(x/pow10[p-1])%10；
}
in int isup(int x) //判断是否在边缘
{
    return x<=3；
}
in int isdown(int x)
{
    return x>=7；
}
in int isleft(int x)
{
    return x%3==1；
}
in int isright(int x)
{
    return x%3==0；
}
in int swap(int x，int a，int b)
{
    int s=get(x，a)，t=get(x，b)；
    x-=s*pow10[a-1]+t*pow10[b-1]；
    x+=s*pow10[b-1]+t*pow10[a-1]；
    return x；
}
in int row(int x)
{
    return (x-1)/3；
}
in int col(int x)
{
    return (x-1)%3；
}
in int f(int state) //估值函数
{
    int s[20]，t[20]；
    memset(s，0，sizeof(s))，memset(t，0，sizeof(t))；
    int ans=0；
    for (int i=1；i<=9；i++) s[get(state，i)]=i，t[get(end，i)]=i；
    for (int i=1；i<=9；i++) ans+=abs(row(s[i])-row(t[i]))+abs(col(s[i])-col(t[i]))； 
    return ans；
}
struct data
{
    int s，w；
    data () {}
    data (int s，int w):s(s)，w(w+f(s)) {}
    bool operator < (const data &rhs) const
    {
        return w>rhs.w；
    }
}；
priority_queue<data> q；
int main()
{
    int s；
    cin>>s；
    q.push(data(s，0))；
    vis.clear()；
    while (!q.empty())
    {
        int p；
        data u=q.top()；q.pop()；
        if (vis[u.s]) continue；
        if (u.s==end) 
        {
            cout<<u.w<<endl；
            return 0；
        }
        vis[u.s]=1；
        for (int i=1；i<=9；i++)
        {
            int x=get(u.s，i)；
            if (!x) 
            {
               p=i；
               break；
            }
        }
        for (int i=0；i<4；i++)
        {
            if (i==0 && isup(p)) continue；
            if (i==1 && isleft(p)) continue；
            if (i==2 && isright(p)) continue；
            if (i==3 && isdown(p)) continue；//判断位置是否合法
            int pp=p+d[i]；
            int t=swap(u.s，p，pp)；
            q.push(data(t，u.w-f(u.s)+1))；
        }
    }
}

结语

A*算法是启发式搜索的一种。事实上除了A*算法外还有IDA*（迭代加深启发式搜索）。在考场上，如果有扎实的搜索功底，是可以拿到很多分的。（毕竟，像最短路算法，dp等，都和搜索有关系。）